Caractéristiques et types de triangle angulaire aigu

Le triangles triangles sont ceux dont les trois angles internes sont des angles aigus; c'est-à-dire que la mesure de chacun de ces angles est inférieure à 90 degrés. N'ayant pas de bon angle, nous avons que le théorème de Pythagore n'est pas rencontré pour cette figure géométrique.

Par conséquent, si nous voulons avoir un type quelconque d'information sur l'un ou l'autre de ses côtés ou de ses angles, il est nécessaire d'utiliser d'autres théorèmes qui nous permettent d'avoir accès auxdites données. Ceux que nous pouvons utiliser sont le théorème de sinus et le théorème de cosinus.

Index

• 1 caractéristiques
  • 1.1 Théorème du sinus
  • 1.2 théorème de cosinus
• 2 types
  • 2.1 triangles triangulaires équilatéraux
  • 2.2 Triangles aigus isocèles
  • 2.3 triangles acután à l'échelle
• 3 Résolution des triangles aigus
  • 3.1 Exemple 1
  • 3.2 Exemple 2
• 4 références

Caractéristiques

Parmi les caractéristiques de cette figure géométrique, on peut souligner celles qui sont données par le simple fait d'être un triangle. Parmi ceux-ci, nous devons:

- Un triangle est un polygone qui a trois côtés et trois angles.

- La somme de ses trois angles internes est égale à 180 °.

- La somme de deux de ses côtés est toujours supérieure à la troisième.

A titre d'exemple, voyons le triangle ABC suivant. En général, nous identifions leurs côtés avec des lettres minuscules et leurs angles avec des majuscules, de sorte qu’un côté et son angle opposé aient la même lettre.

Pour les caractéristiques déjà données, on sait que:

A + B + C = 180 °

a + b> c, a + c> b et b + c> a

La principale caractéristique qui distingue ce type de triangle du reste est que, comme déjà mentionné, ses angles internes sont aigus; c'est-à-dire que la mesure de chacun de ses angles est inférieure à 90 °.

Les triangles acutángulos, ainsi que les triangles obtusángulos (ceux dont l'un des angles a une mesure supérieure à 90 °) font partie de l'ensemble des triangles obliques. Cet ensemble est composé de triangles qui ne sont pas des rectangles.

Lors de la formation de triangles obliques, nous devons utiliser le théorème de sinus et le théorème de cosinus pour résoudre des problèmes impliquant des triangles aigus.

Théorème du sinus

Le théorème du sein indique que le rapport d'un côté au sinus de son angle opposé est égal au double du rayon du cercle formé par les trois sommets de ce triangle. C'est-à-dire:

2r = a / sin (A) = b / sin (B) = c / sin (C)

Théorème de cosinus

Par contre, le théorème du cosinus nous donne ces trois égalités pour tout triangle ABC:

un²= b² + c² -2bc * cos (A)

b²= a² + c² -2ac * cos (B)

c²= a² + b² -2ab * cos (C)

Ces théorèmes sont aussi connus sous le nom de loi du sinus et de la loi du cosinus, respectivement.

Une autre caractéristique que nous pouvons donner des triangles est que deux d'entre eux sont égaux s'ils répondent à l'un des critères suivants:

- S'ils ont les trois côtés égaux.

- S'ils ont un côté et deux angles égaux.

- S'ils ont deux côtés et un angle égal.

Types

Nous pouvons les classer avec des triangles basés sur leurs côtés. Ceux-ci peuvent être:

Triangles équilatéraux triangles

Ce sont les triangles acutángulos qui ont tous les côtés égaux et, par conséquent, tous leurs angles internes ont la même valeur, qui est A = B = C = 60 degrés.

Prenons comme exemple le triangle suivant, dont les côtés a, b et c ont une valeur de 4.

Triangles aigus isocèles

Ces triangles, en plus d'avoir des angles internes aigus, ont la particularité d'avoir deux de leurs côtés égaux et le troisième, qui est généralement considéré comme la base, différent.

Un exemple de ce type de triangles peut être celui dont la base est 3 et ses deux autres côtés ont une valeur de 5. Avec ces mesures, les angles opposés aux côtés égaux avec la valeur de 72,55 ° et l'angle opposé de la base serait 34,9 °.

Echelles acutángulos triangles

Ce sont les triangles qui ont tous deux côtés différents deux à deux. Par conséquent, tous ses angles, en plus d'être inférieurs à 90 °, sont différents de deux à deux.

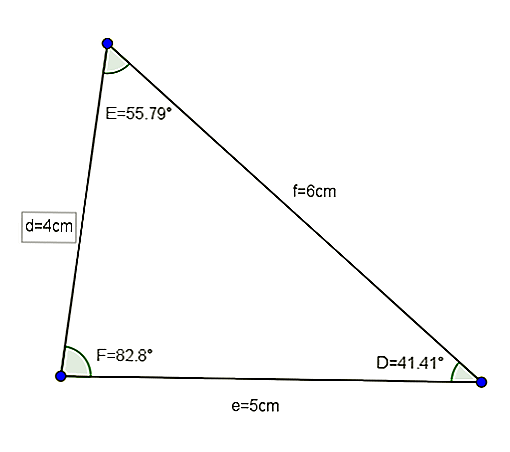
Le triangle DEF (dont les mesures sont d = 4, e = 5 et f = 6 et ses angles sont D = 41,41 °, E = 55,79 ° et F = 82,8 °) est un bon exemple de triangle aigu Scalène

Résolution des triangles aigus

Comme nous l'avons dit précédemment, pour résoudre des problèmes impliquant des triangles aigus, l'utilisation des théorèmes du sinus et du cosinus est nécessaire.

Exemple 1

Étant donné un triangle ABC dont les angles A = 30 °, B = 70 ° et le côté a = 5cm, nous voulons connaître la valeur de l’angle C et des côtés b et c.

La première chose à faire est d'utiliser le fait que la somme des angles internes d'un triangle est de 180 °, afin d'obtenir la valeur de l'angle C.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Nous nettoyons C et nous sommes partis:

C = 180 ° - 100 ° = 80 °

Comme nous connaissons déjà les trois angles et un côté, nous pouvons utiliser le théorème des sinus pour déterminer la valeur des côtés restants. Par le théorème, nous devons:

a / sin (A) = b / sin (B) et a / sin (A) = c / (péché (C)

Nous effaçons b de l'équation et nous devons:

b = (a * sin (B)) / sin (A) ≈ (5 * 0,940) / (0,5) ≈ 9.4

Maintenant, il suffit de calculer la valeur de c. Nous procédons de la même manière que dans le cas précédent:

c = (a * sin (C)) / sin (A) 5 (5 * 0,984) / (0,5) ≈ 9,84

On obtient ainsi toutes les données du triangle. Comme on peut le voir, ce triangle entre dans la catégorie du triangle aigu scalène.

Exemple 2

Étant donné un triangle DEF avec des côtés d = 4cm, e = 5cm et f = 6cm, nous voulons connaître la valeur des angles dudit triangle.

Pour ce cas, nous utiliserons la loi du cosinus, qui nous dit que:

d²= e² + f² - 2efcos (D)

De cette équation, nous pouvons effacer cos (D), ce qui nous donne comme résultat:

Cos (D) = ((4)² - (5)² -(6)²)/(-2*5*6) =0.75

De là nous avons ce D≈ 41.41 °

Maintenant, en utilisant le théorème de senom, nous avons l’équation suivante:

d / (sin (D) = e / (péché (E))

Effacer le péché (E), nous devons:

sin (E) = e * sin (D) / d = (5 * 0,66) / 4 27 0,827

De là, nous avons ce E≈55.79 °

Enfin, en utilisant la somme des angles internes d’un triangle, nous avons cette valeur de F82.8 °.

Références

1. Landaverde, F. d. (1997). Géométrie (édition réimprimée). Progrès
2. Leake, D. (2006). Triangles (éd. Illustrée). Heinemann-Raintree.
3. Leal G. Juan Manuel (2003). Géométrie métrique plana.CODEPRE
4. Ruiz, Á. & Barrantes, H. (2006). Géométries Technologie CR
5. Sullivan, M. (1997). Trigonométrie et géométrie analytique. Pearson Education.